Let $(W,S)$ be a Coxeter system with a based root systems $(\Delta,\Phi)$ on a quadratic space $(V,B)$. Then $W$ is embedded as a subgroup generated by reflections in the group $O(V,B)$ of endomorphism of $V$ preserving the symmetric bilinear form $B$. In particular, $\Phi=W(\Delta)$ is a root system with positive root system $\Phi^+=\textrm{\cone}(\Delta)\cap \Phi$.
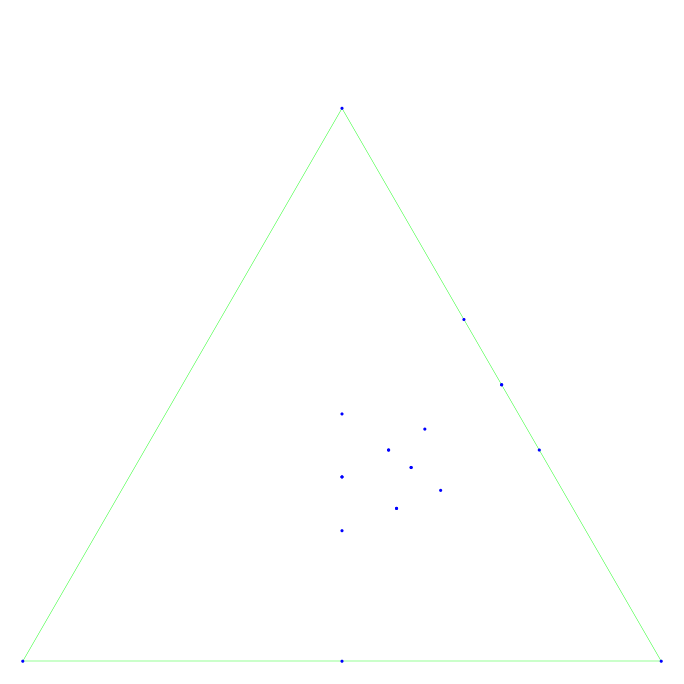
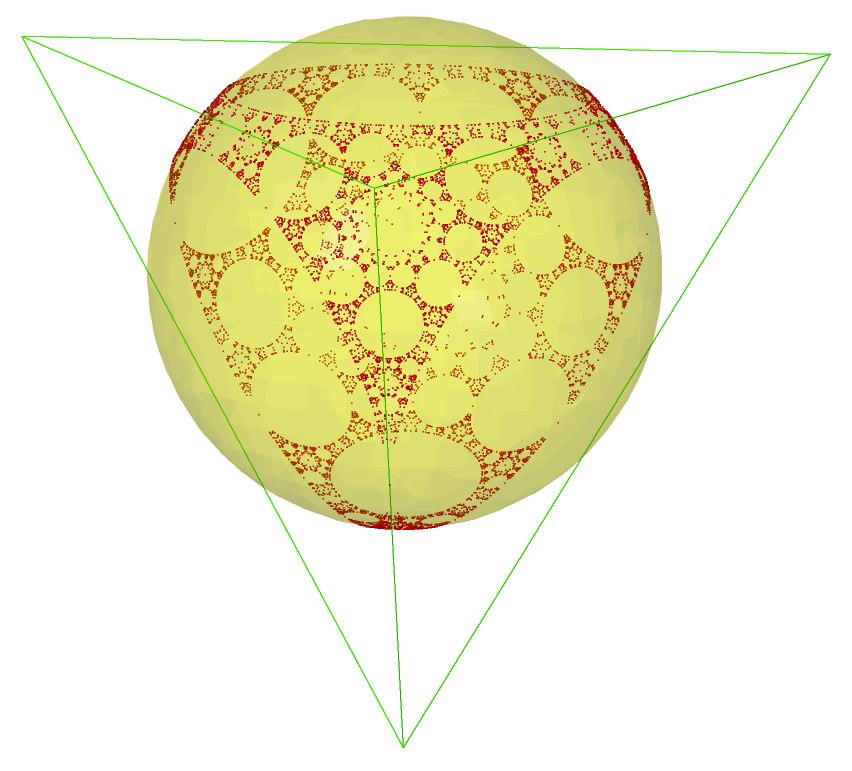
The pictures below represent the projective version of $\Phi$ called a projective root system for $(W,S)$:
$$\mathbb P\Phi = \{\mathbb R\alpha\mid\alpha\in \Phi\}\subseteq \mathbb PV$$
The group $W$ acts on $\mathbb P\Phi$ through the group morphism
$$W\leq O(V,B)\leq GL(V)\rightarrow PGL(V).$$
Therefore, we may see the conic hull $\textrm{\cone}(\Delta)$ becomes the convex hull $\textrm{\con}(\mathbb P\Delta)$ and $\mathbb P\Phi^+=\mathbb P\Phi\subseteq \textrm{\conv}(\Delta)$, which is a polytope (and compact and closed).
We give below examples of projective root system below. This pictures were produces with the help of SageMath and the BROCOLI package by Jean-Philippe Labbé and based on the approach used in these articles:
- Asymptotical behaviour of roots of infinite Coxeter groups, CH with Jean-Philippe Labbé and Vivien Ripoll, Canad. J. Maths 66 (2014), 323-353.
- Imaginary cones and limit roots of infinite Coxeter groups, CH with Matthew Dyer and Vivien Ripoll, Mathematische Zeitschrift, 284(3), 2016, 715-780.
Finite/spherical types (rank 3)
Affine types (rank 3)
$tilde A_2$ 
$tilde C_2$ 
$tilde G_2$
